New
New
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A composite solid can be decomposed to make the volume easier to calculate.
- Completing the solid may be a more useful method.
- Decomposing and rearranging parts of the solid may be beneficial.
Keywords
Volume - The volume is the amount of space occupied by a closed 3D shape.
Compound shape - A compound shape is a shape created using two or more basic shapes. A composite shape is an alternative for compound shape.
Common misconception
Pupils may only using given measures in their calculations, even when these are not the lengths required for substitution into a volume formula.
Encourage pupils to annotate diagrams to show how the are breaking down a compound/composite shape. Pupils should label the diagram with any new lengths needed. They may need to use Pythagoras or trigonometry to find these new lengths.
If some of the measurements are given in different units of length (such as cm and m), encourage the pupils to convert the lengths to the same unit, before starting the volume calculation.

Teacher tip
Licence
This content is © Oak National Academy Limited (2025), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).
Prior knowledge starter quiz
Download quiz pdf
6 Questions
Q1.A shape created using two or more basic shapes is called a shape.
A shape created using two or more basic shapes is called a shape.
Q2.This composite solid is constructed from two cuboids. All lengths given are in centimetres. Calculate the total surface area of the solid.
This composite solid is constructed from two cuboids. All lengths given are in centimetres. Calculate the total surface area of the solid.

456 cm²
912 cm²
982 cm²
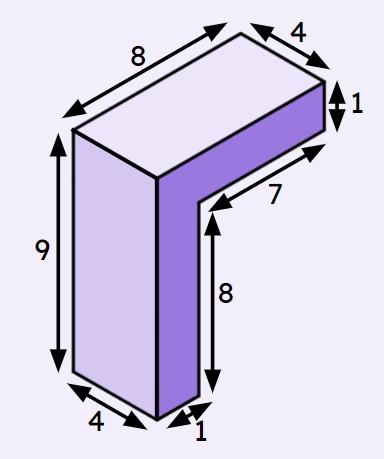
Q3.This composite solid is constructed from two congruent cuboids. All lengths given are in centimetres. The total surface area of the solid is cm².
This composite solid is constructed from two congruent cuboids. All lengths given are in centimetres. The total surface area of the solid is cm².
Q4.The composite solid is constructed by placing a hemisphere with diameter 8 cm on top of a cuboid. Find the surface area of the solid.
The composite solid is constructed by placing a hemisphere with diameter 8 cm on top of a cuboid. Find the surface area of the solid.
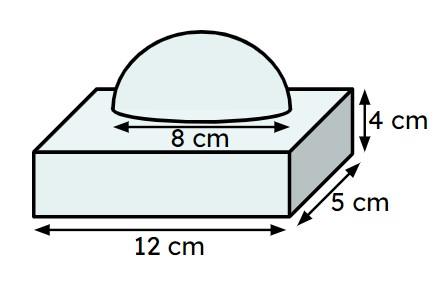
206 cm²
357 cm²
407 cm²
Q5.The composite solid is constructed with a cylinder and a hemisphere. Each have a diameter of 12 cm. Find the surface area of the solid.
The composite solid is constructed with a cylinder and a hemisphere. Each have a diameter of 12 cm. Find the surface area of the solid.

792 cm²
829 cm²
867cm²
1018 cm²
Q6.The composite solid is constructed with a cone and a hemisphere. The surface area, in terms of 𝜋, is 𝜋 cm².
The composite solid is constructed with a cone and a hemisphere. The surface area, in terms of 𝜋, is 𝜋 cm².

Assessment exit quiz
Download quiz pdf
6 Questions
Q1.The amount of space occupied by a closed 3D shape is called the of the shape.
The amount of space occupied by a closed 3D shape is called the of the shape.
Q2.The diagram shows a composite solid constructed from two congruent cuboids. All lengths given are in centimetres. Which of these calculations give the total volume of the solid?
The diagram shows a composite solid constructed from two congruent cuboids. All lengths given are in centimetres. Which of these calculations give the total volume of the solid?

4 × 2 × 8 + 2 × 4 × 8
6 × 4 × 8
Q3.This composite solid is constructed from two cuboids. All lengths given are in metres. The total volume of the solid is m³.
This composite solid is constructed from two cuboids. All lengths given are in metres. The total volume of the solid is m³.

Q4.This composite solid is constructed by placing a hemisphere with diameter 12 cm on top of a cuboid. Find the volume of the solid. Give your answer to the nearest cubic centimetre.
This composite solid is constructed by placing a hemisphere with diameter 12 cm on top of a cuboid. Find the volume of the solid. Give your answer to the nearest cubic centimetre.

631 cm³
1385 cm³
4099 cm³
Q5.This composite solid is constructed with a cylinder and a hemisphere. Each have a diameter of 8 cm. The volume of the solid is cm³ (correct to 3 significant figures).
This composite solid is constructed with a cylinder and a hemisphere. Each have a diameter of 8 cm. The volume of the solid is cm³ (correct to 3 significant figures).

Q6.This composite solid is constructed with a cone and a hemisphere. The volume of the solid, in terms of 𝜋, is 𝜋 cm³.
This composite solid is constructed with a cone and a hemisphere. The volume of the solid, in terms of 𝜋, is 𝜋 cm³.



