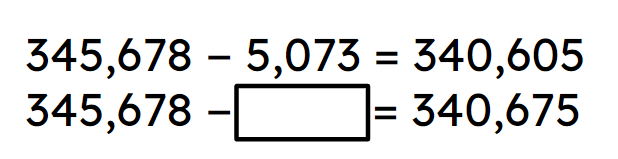New
New
Lesson 9 of 10
Calculate the difference using knowledge of an adjusted subtrahend: difference structure
I can calculate the difference using knowledge of an adjusted subtrahend in a difference structure
Lesson 9 of 10
New
New
Calculate the difference using knowledge of an adjusted subtrahend: difference structure
I can calculate the difference using knowledge of an adjusted subtrahend in a difference structure
Lesson details
Key learning points
- The more you subtract the smaller the difference.
- The less you subtract the greater the difference.
- A number line can be used to represent the change in the subtrahend.
Keywords
Minuend - The minuend is the number being subtracted from.
Subtrahend - A subtrahend is a number subtracted from another.
Difference - The difference is the result after subtracting one number from another.
Adjust - When you adjust you make a change to a number. This is done to make a calculation easier to solve mentally.
Common misconception
Many pupils will try to adjust the difference in the same way that the subtrahend has been adjusted without considering the use of the inverse.
Start simply with double-sided counters to show the concept practically.
You can get the children to create their own sequences of equations with missing numbers to solve for one another. Give certain parameters to avoid overly complex numbers and make sure they know to alternate between concealing the subtrahend or difference each time.

Teacher tip
Licence
This content is © Oak National Academy Limited (2025), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).
Prior knowledge starter quiz
Download quiz pdf
6 Questions
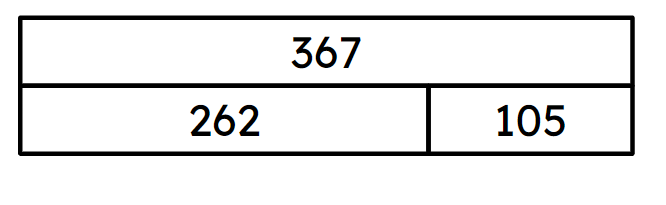
Q1.If the subtrahend is 262, which part of the bar model below is the difference?
If the subtrahend is 262, which part of the bar model below is the difference?
367
262
Q2.Solve the following calculation mentally by adjusting the minuend and subtrahend.
285 − 77 =
Solve the following calculation mentally by adjusting the minuend and subtrahend.
285 − 77 =
Q3.Solve the following calculation mentally using unitisation.
= 3,900 − 1,300
Solve the following calculation mentally using unitisation.
= 3,900 − 1,300
Q4.Solve the following calculation mentally by adjusting the minuend and then the difference.
4,008 − 1,300 =
Solve the following calculation mentally by adjusting the minuend and then the difference.
4,008 − 1,300 =
Q5.Solve the following calculation using a mental strategy.
= 703 − 146
Solve the following calculation using a mental strategy.
= 703 − 146
Q6.Look at the jottings. What was the value of the adjustment to the subtrahend and the difference?
Look at the jottings. What was the value of the adjustment to the subtrahend and the difference?
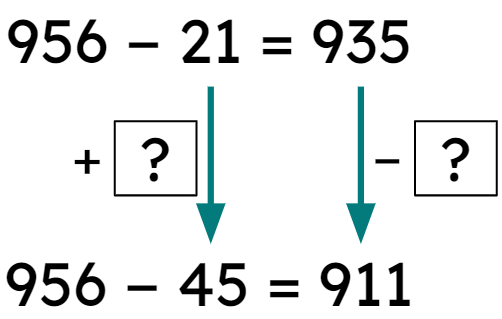
Assessment exit quiz
Download quiz pdf
6 Questions
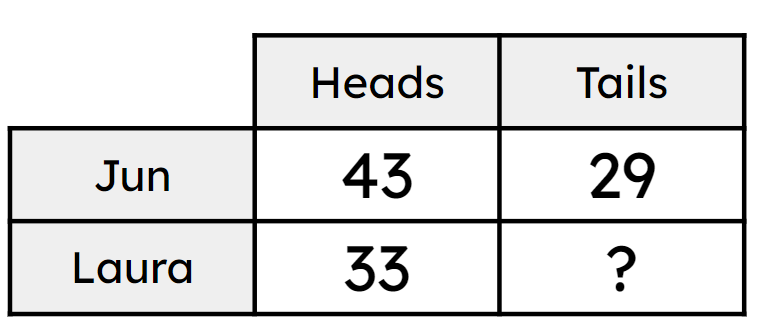
Q1.Jun and Laura are flipping coins and recording the results as they go. They each flip the coin 72 times. The table shows how many they each got except one blank cell. How many tails did Laura get?
Jun and Laura are flipping coins and recording the results as they go. They each flip the coin 72 times. The table shows how many they each got except one blank cell. How many tails did Laura get?
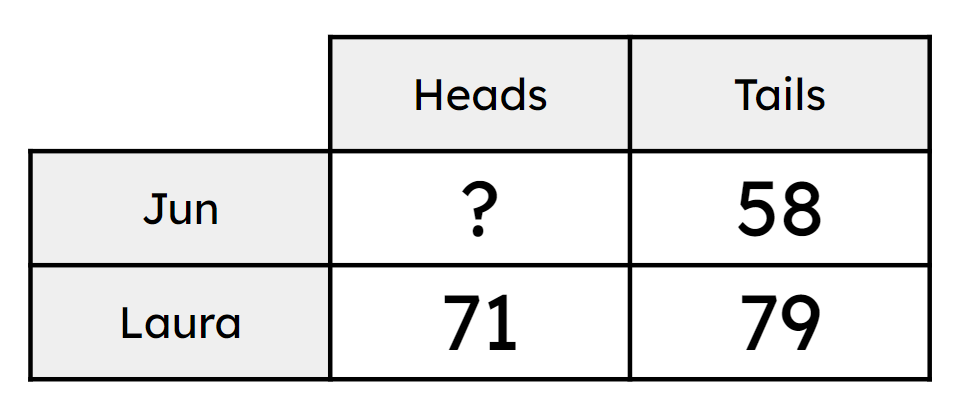
Q2.Jun and Laura are flipping coins and recording the results as they go. They each flip the coin 150 times. The table shows how many they each got except one blank cell. How many heads did Jun get?
Jun and Laura are flipping coins and recording the results as they go. They each flip the coin 150 times. The table shows how many they each got except one blank cell. How many heads did Jun get?
Q3.Jun and Laura each take the same number of shots at the goal ring in netball. Jun scores 20 Laura scores 17 but misses 18 How many did Jun miss? misses
Jun and Laura each take the same number of shots at the goal ring in netball. Jun scores 20 Laura scores 17 but misses 18 How many did Jun miss? misses
Q4.Jun and Laura each take the same number of shots at the goal ring in netball. Laura misses 32 and scores 21 Jun misses 16 only. How many did Jun score? Jun scored
Jun and Laura each take the same number of shots at the goal ring in netball. Laura misses 32 and scores 21 Jun misses 16 only. How many did Jun score? Jun scored
Q5.Look at the pair of equations and use the complete one to help find the missing number in the second.
Look at the pair of equations and use the complete one to help find the missing number in the second.
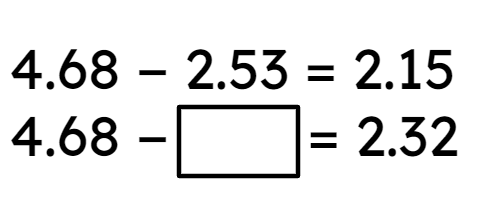
Q6.Look at the pair of equations below and use the complete one to help find the missing number in the second.
Look at the pair of equations below and use the complete one to help find the missing number in the second.