Year 7
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
These resources were created for remote use during the pandemic and are not designed for classroom teaching.
Lesson details
Key learning points
- In this lesson, we will learn how to establish inequalities from perimeter expressions.
Licence
This content is made available by Oak National Academy Limited and its partners and licensed under Oak’s terms & conditions (Collection 1), except where otherwise stated.
5 Questions
Q1.
Perimeter is the total _____ of all sides of a shape. When the side lengths are written algebraically the perimeter can be written as an _______.
length, equation
weight, equation
weight, expression
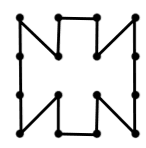
Q2.
Which of the following is an expression for the perimeter of this shape? (Use the definitions from the lesson.)
4p + 2q
6p
6q
Q3.
Which of the following is an expression for the perimeter of this shape? (Use the definitions from the lesson.)
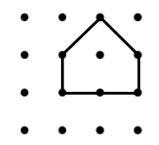
2p + 4q
6p
6q
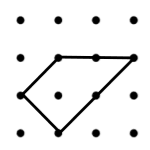
Q4.
Which of the following is an expression for the perimeter of this image? (Use the definitions from the lesson.)
12p + 2q
16pq
6p + 10q
Q5.
Which of the following is an expression for the perimeter of this image? (Use the definitions from the lesson.)
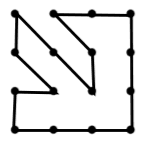
12p + 2q
16pq
6p + 10q
5 Questions
Q1.
Fill in the gap: We can use an ______ to compare the lengths and perimeters of different lines and shapes.
Equality
Equation
Expression
Q2.
Using the image, decide which of the following is true.
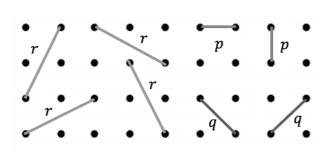
r < p
r < q
r = q
Q3.
Which inequality best compares the expressions for the perimeters of the 2 shapes below?
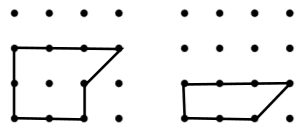
8p + q < 6p + q
8q + p < 6q + p
8q + p > 6q + p
Q4.
Which inequality best compares the expressions for the perimeters of the 2 shapes below?
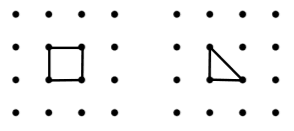
4p < 2p + q
4p < 3p
4p > 3p
Q5.
Which inequality best compares the expressions for the perimeters of the 2 shapes below?
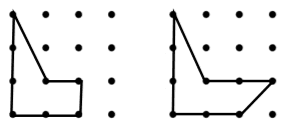
7p + q < 7p + 2q
7p + q > 7p + 2q
7p + r > 7p + q + r

