Myths about teaching can hold you back


- Year 8
Perpendicular to a given line through a given point
I can use the properties of a rhombus to construct a perpendicular to a given line through a given point.


- Year 8
Perpendicular to a given line through a given point
I can use the properties of a rhombus to construct a perpendicular to a given line through a given point.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A rhombus can be constructed from two congruent isosceles triangles.
- This can be used to construct a perpendicular to a line through a point.
- This perpendicular has special properties that can be investigated.
- Shortest distances can be found using constructions with perpendicular lines.
Keywords
Bisect - To bisect means to cut or divide an object into two equal parts.
Rhombus - A rhombus is a parallelogram where all sides are the same length.
Common misconception
You can't accurately draw the perpendicular to a point on a line segment close to its endpoint.
The perpendicular to a line segment through any point can be found; some line segments just require extending in length first.
To help you plan your year 8 maths lesson on: Perpendicular to a given line through a given point, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 8 maths lesson on: Perpendicular to a given line through a given point, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 3 maths lessons from the Constructions unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
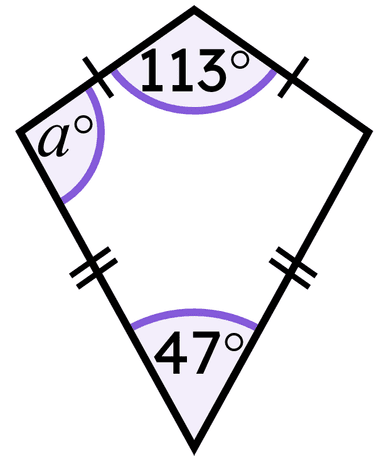
Q1.This quadrilateral is a kite. Find the value of angle $$a$$, in degrees.
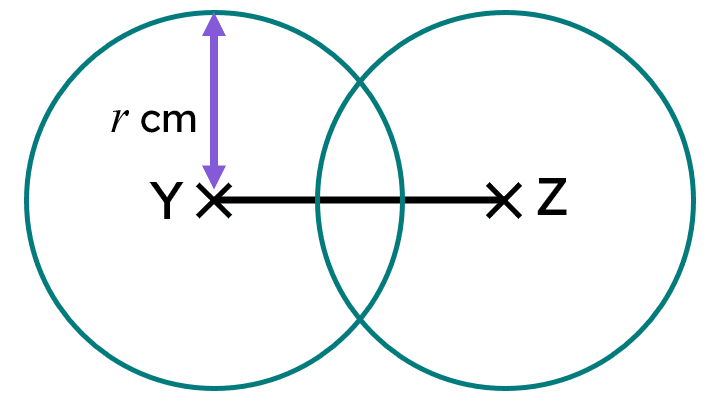
Q2.This diagram shows an accurate construction of a perpendicular bisector. YZ has a length of 8.4 cm. Which of these is the smallest value of $$r$$ that can be used in this construction?
Q3.Match the sentence to the diagram.
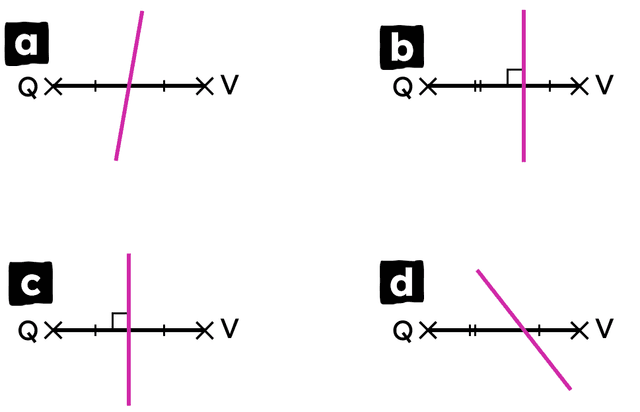
a -
A bisector to line segment QV
b -
A perpendicular to line segment QV
c -
A perpendicular bisector to line segment QV
d -
An intersecting line to line segment QV
Q4.This is an incomplete construction to find the perpendicular bisector of YZ. Which of these steps is missing from this construction?
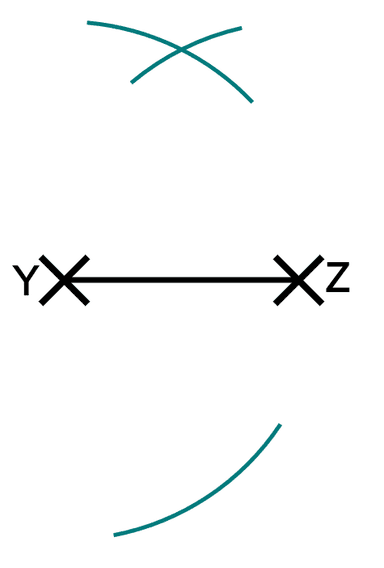
Q5.This is an accurate construction to draw a rhombus. What is the perimeter (in cm) of the rhombus that can be drawn from this construction?
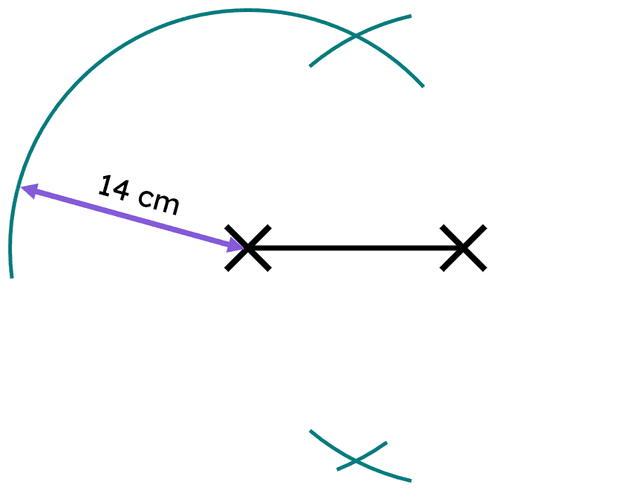
Q6.Sofia starts her construction of a perpendicular bisector to EF. She is about to move the pair of compoasses to construct a second circle. Which of these statements are true?
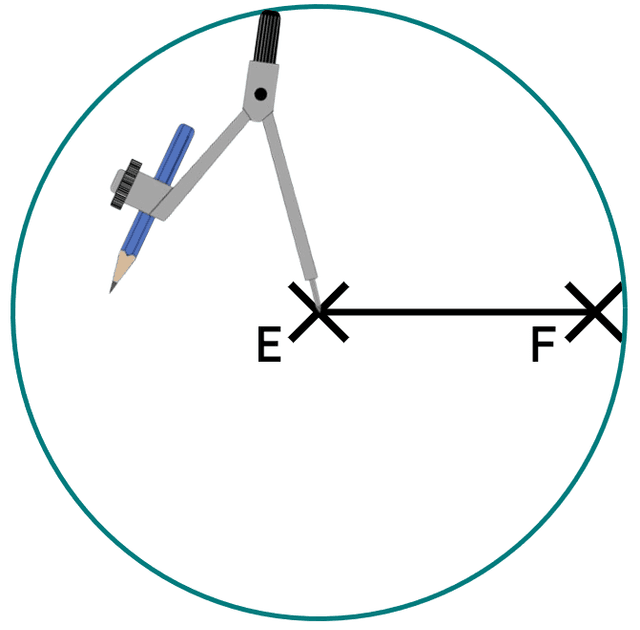
Assessment exit quiz
6 Questions
Q1.The line segment EF has been shortened by constructing a circle of radius 8 cm, with a centre at point K. What is the length (in cm) of the shortened line segment?
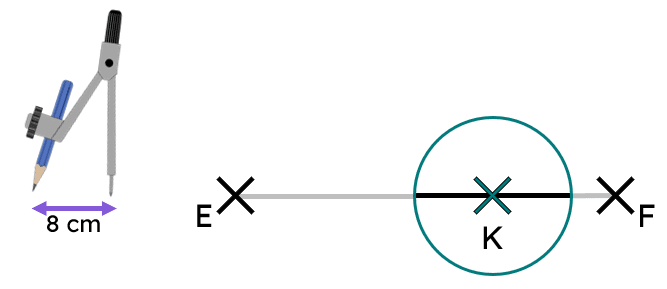
Q2.Which of these diagrams shows the most appropriate first step when constructing the perpendicular to line segment TU through point Z?
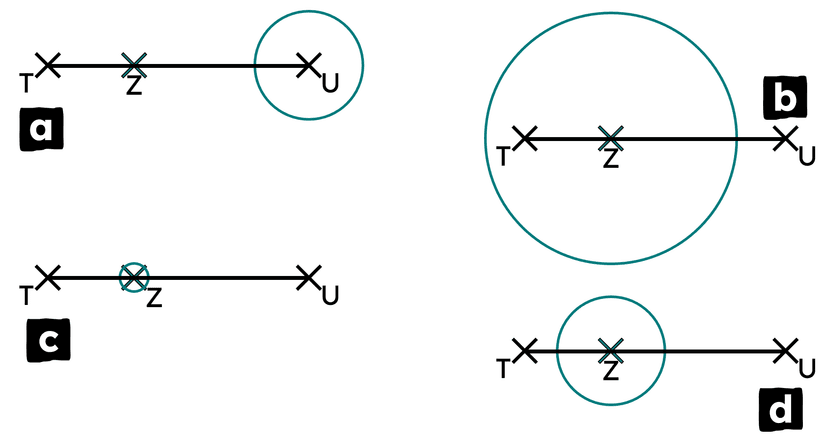
Q3.Izzy has shortened line segment LM by drawing a circle with centre at point Z. Izzy wants to draw four arcs of radius $$k$$ cm to construct a perpendicular. What value must $$k$$ be greater than?
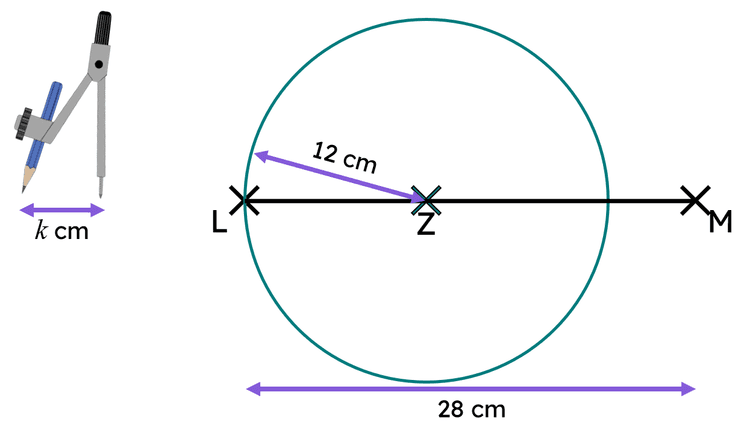
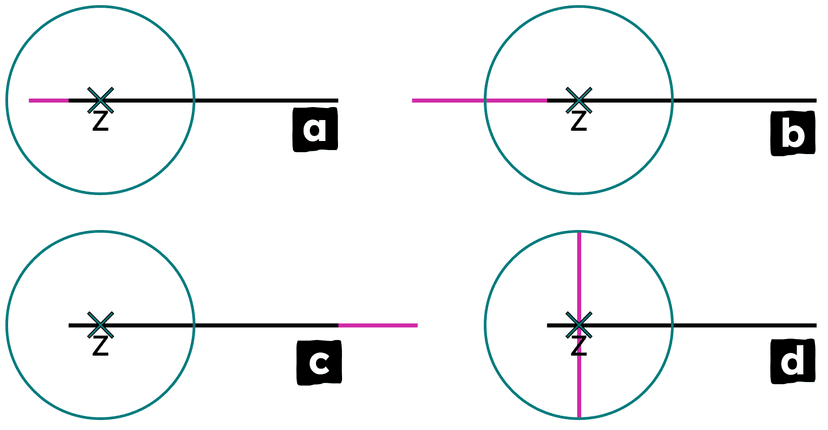
Q4.A line segment is extended so that a perpendicular can be constructed through point Z. Which of these diagrams shows a suitable extension of the line segment?
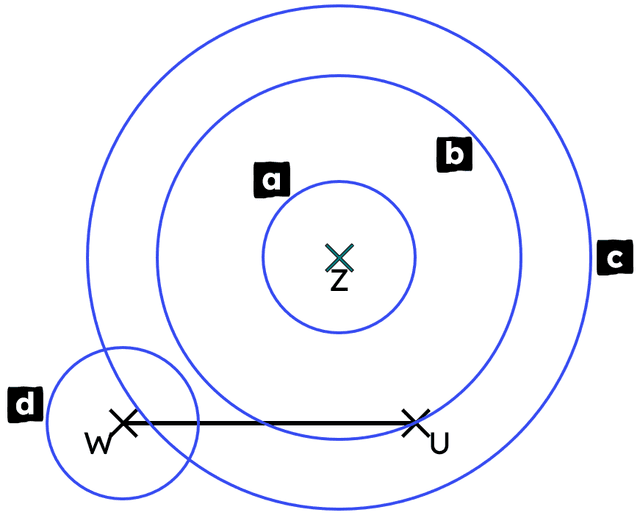
Q5.Which of these four circles can help in the construction of the perpendicular to line segment WU through point Z?
Q6.Match the values to their statements.
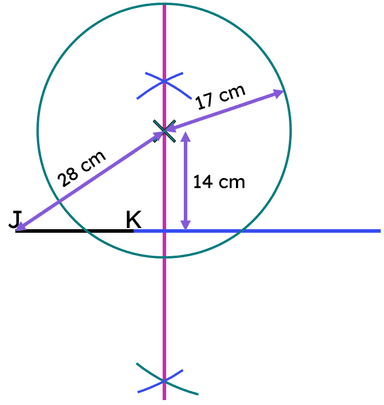
14 cm -
the shortest distance from X to an extension of JK
15 cm -
the shortest distance from X to line segment JK
17 cm -
the radius of circle with centre at point X
28 cm -
the shortest distance from X to point J

