New
New
Year 10
Foundation
Checking and securing understanding of direct proportion in context
I can recognise direct proportion in a range of contexts, including compound measures.
New
New
Year 10
Foundation
Checking and securing understanding of direct proportion in context
I can recognise direct proportion in a range of contexts, including compound measures.
Lesson details
Key learning points
- Direct proportion can be used in a number of contexts.
- One context is converting compound measure.
- Another is currency conversion.
- Regardless of the context, if one quantity is zero, the other must be as well.
- It is useful to be able to recognise which contexts involve direct proportion.
Common misconception
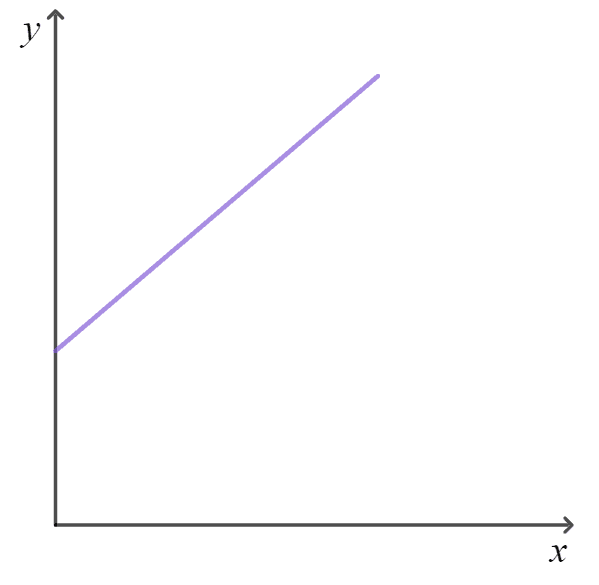
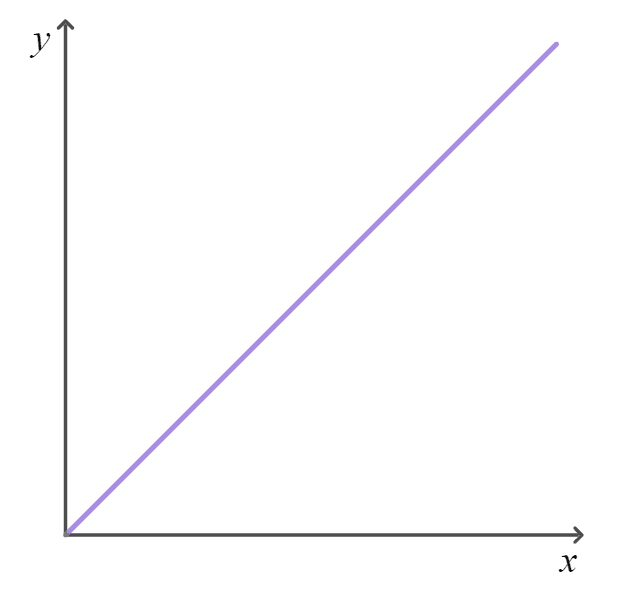
All straight line graphs show direct proportion.
Only straight line graphs that pass through the origin (0, 0) show direct proportion.
Keywords
Direct proportion - Two variables are in direct proportion if they have a constant multiplicative relationship.
Licence
This content is © Oak National Academy Limited (2024), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).
Video
Loading...
Starter quiz
Download starter quiz
6 Questions
Q1.
Two variables are in proportion if they have a constant multiplicative relationship.
Q2.
Four friends went to the cinema. The cost of their tickets was £38. How much did each ticket cost? £
Q3.
In a supermarket, 3 tins of soup cost £4.80. 8 tins of the same soup should cost £
Q4.
Match each measurement to its equivalent measurement.
33 mm
3.03 m
0.33 cm
3300 mm
3300 cm
Q5.
Calculate the volume of this cuboid.
0.9 m³
9 m³
1.47 m³
132.15 m³
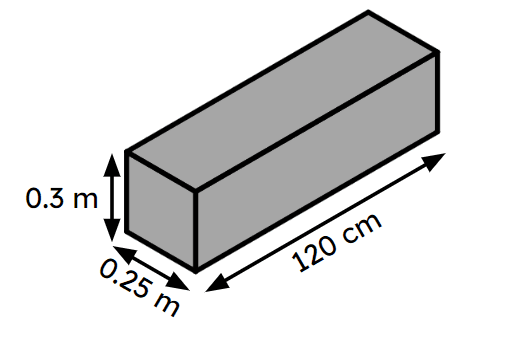
Q6.
Calculate the surface area of this cuboid.
0.09 m²
0.735 m²
2.94 m²
Exit quiz
Download exit quiz
6 Questions
Q1.
Two variables are in direct proportion if they have a __________ relationship.
additive
constant multiplicative
multiplicative
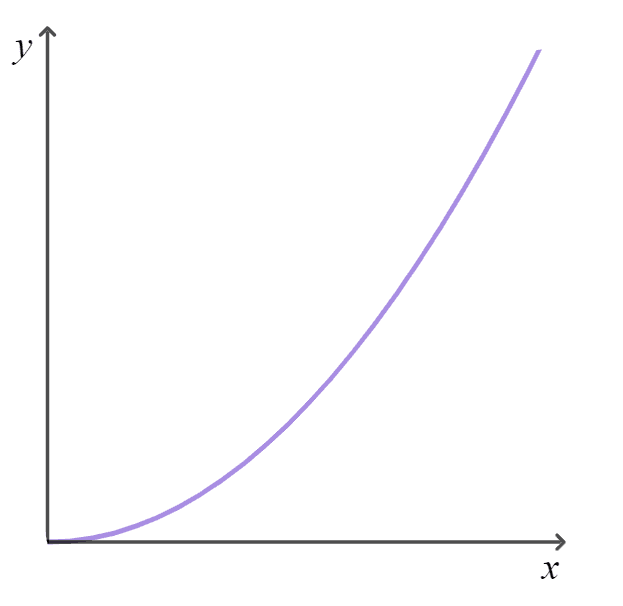
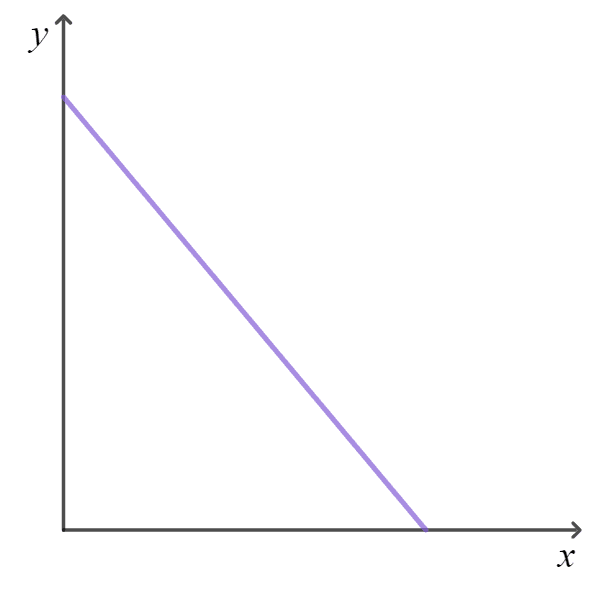
Q2.
Which of these graphs shows direct proportion between the two variables?
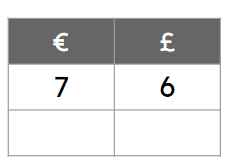
Q3.
The ratio table shows the conversion €7 (Euros) = £6 (Pounds Sterling). €630 = £
Q4.
The perimeter of a triangle is 33 300 cm. Which calculation shows its perimeter in metres?
33 300 cm ÷ 10
33 300 cm ÷ (3 × 100)
33 300 cm ÷ 100 ÷ 100 ÷ 100
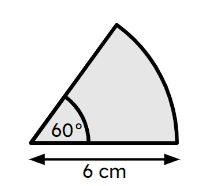
Q5.
A circular sector with an angle of 60° has a radius of 6 cm, an arc length of 2π cm and an area of 6π cm². Select the correct statements.
The area is directly proportional to the radius.
If the radius is doubled, the area will be 12π cm².
Q6.
The area of a triangle is 600 cm². The area of the triangle in metres squared is m².