Year 11
Higher
Volume: Further problem solving with spheres, cones and pyramids
Year 11
Higher
Volume: Further problem solving with spheres, cones and pyramids
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
These resources were created for remote use during the pandemic and are not designed for classroom teaching.
Lesson details
Key learning points
- In this lesson, we will further our problem solving with volume of spheres, cones and pyramids which also uses Pythagoras' Theorem to find missing lengths.
Licence
This content is made available by Oak National Academy Limited and its partners and licensed under Oak’s terms & conditions (Collection 1), except where otherwise stated.
3 Questions
Q1.
Amy is working out the volume of this hemisphere. What mistake has Amy made?

Amy has not halved the volume of the sphere.
Amy has not used the correct formula for volume.
Q2.
Work out the total surface area for this hemisphere rounded to 1 decimal place.
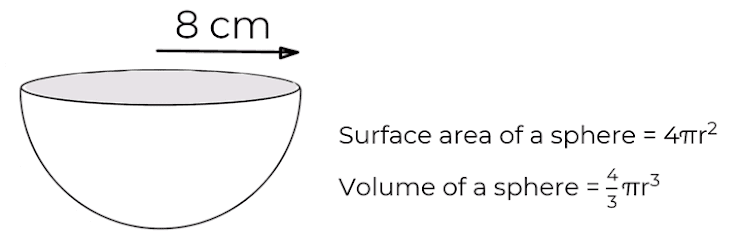
1005.3 cm²
402.1 cm²
804.2 cm²
Q3.
Work out the volume of this hemisphere rounded to 1 decimal place.
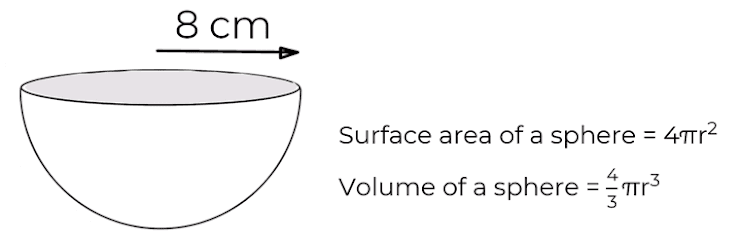
134.0 cm³
2144.7 cm³
8578.6 cm³
3 Questions
Q1.
If a solid metal sphere with radius 90 cm was melted down to make smaller spheres of with 3 cm radius, how many smaller spheres could be made?
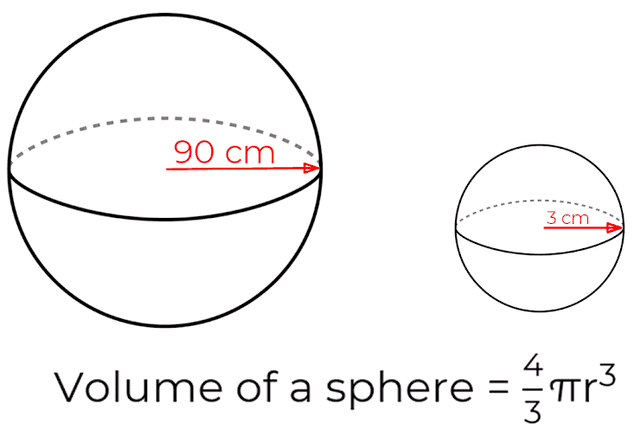
30
300
900
Q2.
The diagram shows a pencil crayon. The sharpened part of the pencil forms a cone attached to a cylindrical main part of the pencil. Work out the total volume of the pencil crayon to the nearest cm³.
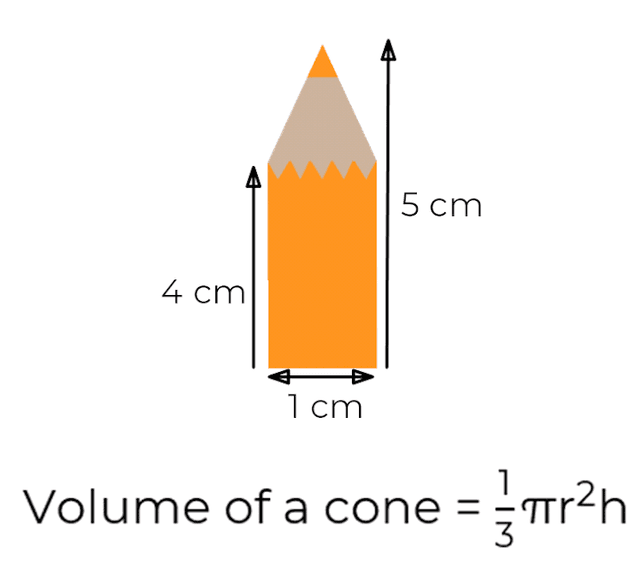
13 cm³
29 cm³
5 cm³
Q3.
The diagram shows a square based pyramid with a perpendicular height of 30 cm. Work out the volume of the pyramid.
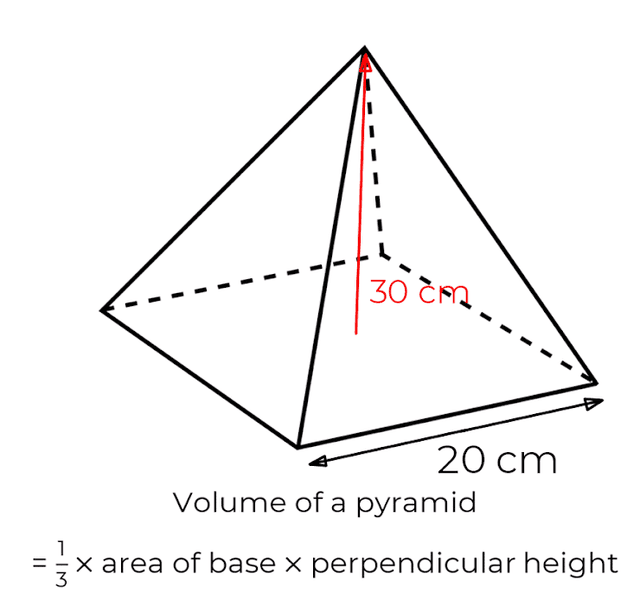
12,000 cm³
600 cm³
8000 cm³

