Skip to content
Oak National Academy
Oak National Academy
Teachers
Pupils
New
New
Year 4

Add mixed numbers crossing the whole

I can add mixed numbers crossing the whole.

Download all resources
arrow-right
Share activities with pupils
arrow-right
New
New
Year 4

Add mixed numbers crossing the whole

I can add mixed numbers crossing the whole.

Download all resources
arrow-right
Share activities with pupils
arrow-right
warning

These resources will be removed by end of Summer Term 2025.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
View new resources
arrow-right

Lesson details

Key learning points

  1. Improper fractions can be added in the same way as proper fractions.
  2. A mixed number can be partitioned into its parts when adding it to improper or proper fractions.
  3. To add two mixed numbers, the whole number parts can be added and the fractional parts can be added.
  4. If the sum has a fractional part greater than one, this needs a conversion to express it as a conventional mixed number.
  5. A number line is a useful tool to use to support addition of mixed numbers.

Keywords

  • Mixed number - A mixed number is a whole number and a fraction combined.

  • Improper fraction - An improper fraction is a fraction where the numerator is greater than or equal to the denominator.

Common misconception

Adding the fractional part of a mixed number to a proper fraction may result in an improper fraction, which may be recombined with the whole number part of the mixed number and left as improper.

In a mixed number, the numerator of the fractional part must always be smaller than the denominator. If it is greater, a final conversion is needed.

Children need to have a secure understanding of how to add proper fractions to enable them to successfully add improper fractions.
Teacher tip

Licence

This content is © Oak National Academy Limited (2024), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).

Lesson video

Skip lesson video

Loading...

Starter quiz

Download starter quiz

6 Questions

Q1.
The whole has been divided into six equal parts, each part is one- of the whole.
An image in a quiz
Correct Answer: sixth
Q2.
Select the mixed numbers.
$$ {9} \over {7}$$
Correct answer: $$1{{3} \over {7}}$$
$$ {3} \over {7}$$
$$ {13} \over {7}$$
Correct answer: $$ 4{{1} \over {7}}$$
Q3.
$$ {3} \over {10}$$ + $$ {4} \over {10}$$ =
$$ {1} \over {10}$$
Correct answer: $$ {7} \over {10}$$
$$ {1} \over {20}$$
$$ {7} \over {20}$$
$$ {34} \over {20}$$
Q4.
Match the expressions to their sum.
Correct Answer:$$ {1} \over {4}$$ + $$ {1} \over {4}$$,$$ {2} \over {4}$$

$$ {2} \over {4}$$

Correct Answer:$$ {1} \over {4}$$ + $$ {2} \over {4}$$,$$ {3} \over {4}$$

$$ {3} \over {4}$$

Correct Answer:$$ {1} \over {5}$$ + $$ {2} \over {5}$$,$$ {3} \over {5}$$

$$ {3} \over {5}$$

Correct Answer:$$ {1} \over {5}$$ + $$ {3} \over {5}$$,$$ {4} \over {5}$$

$$ {4} \over {5}$$

Correct Answer:$$ {2} \over {8}$$ + $$ {2} \over {8}$$,$$ {4} \over {8}$$

$$ {4} \over {8}$$

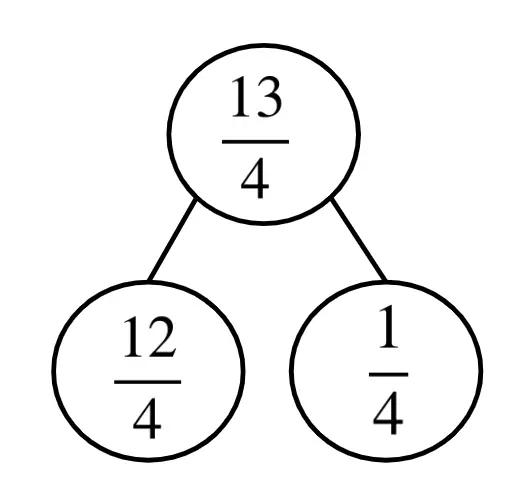
Q5.
Use the part-part-whole model to express $$ {13} \over {4}$$ as a mixed number.
An image in a quiz
$$ {1} \over {4}$$
$$ {12} \over {4}$$
$$1{{1} \over {4}}$$
$$2{{1} \over {4}}$$
Correct answer: $$3{{1} \over {4}}$$
Q6.
Match the improper fractions to their equivalent mixed number.
Correct Answer:$$ {9} \over {4}$$ ,$$2{{1} \over {4}}$$

$$2{{1} \over {4}}$$

Correct Answer:$$ {18} \over {4}$$ ,$$4{{2} \over {4}}$$

$$4{{2} \over {4}}$$

Correct Answer:$$ {29} \over {4}$$ ,$$7{{1} \over {4}}$$

$$7{{1} \over {4}}$$

Correct Answer:$$ {34} \over {4}$$ ,$$8{{2} \over {4}}$$

$$8{{2} \over {4}}$$

Correct Answer:$$ {46} \over {4}$$ ,$$11{{2} \over {4}}$$

$$11{{2} \over {4}}$$

Exit quiz

Download exit quiz

6 Questions

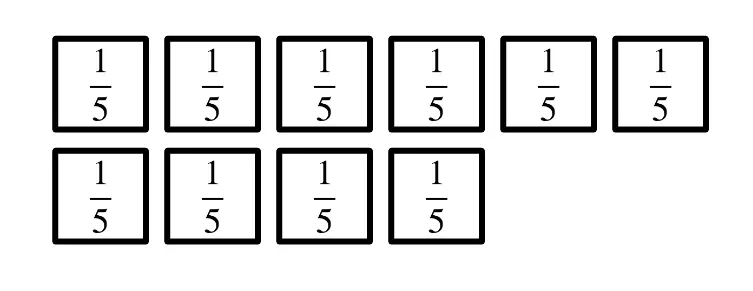
Q1.
Find the total value of the rods. Give your answer as a whole number if you can.
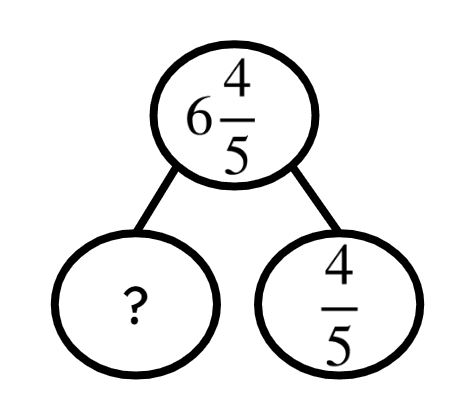
An image in a quiz
Correct Answer: 2, 10 fifths
Q2.
Complete the part-part-whole model.
An image in a quiz
Correct Answer: 6
Q3.
$$6{{4} \over {5}}$$ + $$ {3} \over {5}$$ = ?
Correct answer: $$6{{7} \over {5}}$$
$$6{{8} \over {10}}$$
Correct answer: $$7{{2} \over {5}}$$
$$7{{3} \over {10}}$$
Q4.
Calculate $$1{{8} \over {9}}$$ + $$ {3} \over {9}$$ giving your answer as a conventional mixed number.
$$1{{11} \over {9}}$$
$$1{{11} \over {18}}$$
Correct answer: $$2{{2} \over {9}}$$
$$2{{11} \over {9}}$$
Q5.
Calculate $$2{{8} \over {10}}$$ + $$1{3} \over {10}$$ giving your answer as a conventional mixed number.
$$2{{11} \over {10}}$$
$$3{{11} \over {10}}$$
$$3{{11} \over {20}}$$
$$4{{11} \over {10}}$$
Correct answer: $$4{{1} \over {10}}$$
Q6.
Match the expression to its sum.
Correct Answer:$$4{{1} \over {9}}$$,$$2{{7} \over {9}}$$ + $$1{{3} \over {9}}$$

$$2{{7} \over {9}}$$ + $$1{{3} \over {9}}$$

Correct Answer:$$2{{8} \over {9}}$$,$$1{{5} \over {9}}$$ + $$1{{3} \over {9}}$$

$$1{{5} \over {9}}$$ + $$1{{3} \over {9}}$$

Correct Answer:4,$$3{{4} \over {9}}$$ + $$ {5} \over {9}$$

$$3{{4} \over {9}}$$ + $$ {5} \over {9}$$

Correct Answer:5,$$3{{4} \over {9}}$$ + $$1{{5} \over {9}}$$

$$3{{4} \over {9}}$$ + $$1{{5} \over {9}}$$

Correct Answer:$$4{{2} \over {9}}$$,$$1{{3} \over {9}}$$ + $$2{8} \over {9}$$

$$1{{3} \over {9}}$$ + $$2{8} \over {9}$$