Myths about teaching can hold you back
- Year 4
Represent division by sharing with equations
I can represent and interpret division by sharing where there is a remainder.
- Year 4
Represent division by sharing with equations
I can represent and interpret division by sharing where there is a remainder.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A multiplication and addition equation can be written to represent division between groups (or sharing).
- A division equation can be written to represent division between groups (or sharing).
- The number of equal groups to share out can be found by counting forwards.
- The number of equal groups to share out can be found by counting backwards.
- Counting forwards is usually easier because multiplication facts can be used to help us.
Keywords
Share - Sharing is when a whole amount is split into equal parts or groups. We know the total number of objects and the number of parts it is split into, but we don't know how many are in each part.
Remainder - A remainder is the amount left over after division when the dividend does not divide exactly by the divisor.
Division - Division is splitting into equal parts or groups.
Common misconception
Children may not see the link between sharing and grouping as sharing has traditionally been done by sharing out objects one by one. This becomes far less efficient when working with larger numbers.
To develop understanding of 'dividing between', ensure that physical objects are shared out in groups each time (forming an array beneath a bar model), rather than one by one.
To help you plan your year 4 maths lesson on: Represent division by sharing with equations, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 4 maths lesson on: Represent division by sharing with equations, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 2 maths lessons from the Division with remainders unit, dive into the full primary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
Q1.There are 30 children. Which equal-sized groups could they get into without any children being left out?
Q2.Match the multiplication and division equations that represent the same number of groups.
24 ÷ 8 = 3
30 ÷ 5 = 6
63 ÷ 9 = 7
56 ÷ 7 = 8
Q3.Jun had 36 stickers. He could fit 6 stickers on each page of his book. How many pages did he fill with his stickers? pages
Q4.Match the multiplication and division equations with remainders that could represent the same number of groups.
5 × 4 + 2
6 × 5 + 4
4 × 6 + 2
7 × 4 + 3
Q5.Sofia has 38 cakes and each plate can hold 8 cakes. Which of these statements is correct?
Q6.Jun had 43 books. He could fit 5 books onto each shelf of his bookshelf. How many books would not fit onto a shelf?
Assessment exit quiz
6 Questions
Q1.Look at the division equation. Match the numbers to the description.
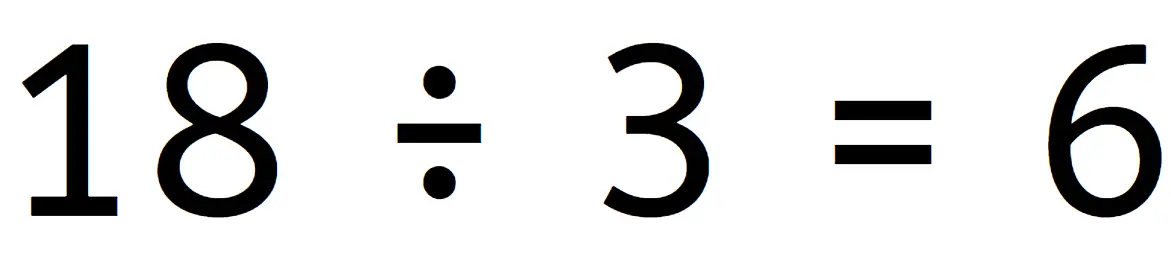
the dividend
the divisor
the quotient
Q2.Look at the division and multiplication equations. What number is missing from both?
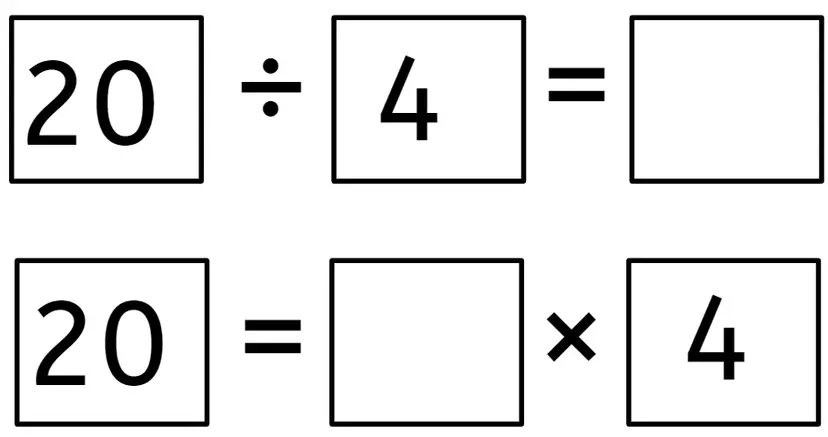
Q3.Which equations could this number line represent?

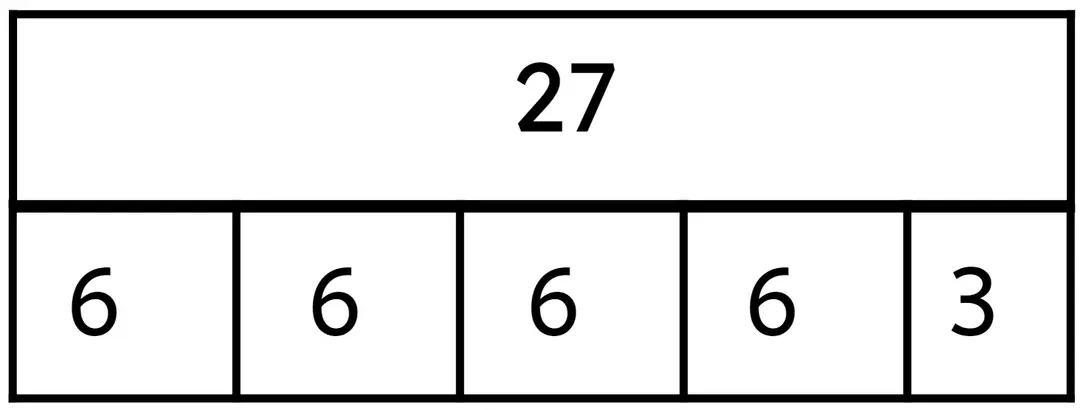
Q4.Look at the bar model. Which equations could it represent?